laminärt och turbulent flöde

egenskaperna hos laminärt och turbulent flöde är mycket olika. För att förstå varför turbulent eller laminärt flöde är önskvärt vid driften av ett visst system är det nödvändigt att förstå egenskaperna hos laminärt och turbulent flöde.,

flödessystem

allt vätskeflöde klassificeras i en av två breda kategorier eller regimer. Dessa två flödesregimer är laminärt flöde och turbulent flöde. Flödesregimen, vare sig laminär eller turbulent, är viktig vid utformningen och driften av något vätskesystem. Mängden vätskefriktion, som bestämmer den mängd energi som krävs för att bibehålla det önskade flödet, beror på flödesläget. Detta är också en viktig faktor i vissa tillämpningar som innebär värmeöverföring till vätskan.,

laminärt flöde

laminärt flöde kallas också streamline eller visköst flöde. Dessa termer är beskrivande av flödet eftersom, i laminärt flöde, (1) skikt av vatten som strömmar över varandra vid olika hastigheter med praktiskt taget ingen blandning mellan skikt, (2) vätskepartiklar rör sig i bestämda och observerbara vägar eller streamlines, och (3) flödet är karakteristisk för viskös (tjock) vätska eller är en i vilken viskositeten hos vätskan spelar en betydande roll.

Turbulent flöde

Turbulent flöde kännetecknas av oregelbunden rörelse av partiklar av vätskan., Det finns ingen bestämd frekvens eftersom det finns i vågrörelse. Partiklarna färdas i oregelbundna banor utan observerbart mönster och inga bestämda lager.

Flödeshastighetsprofiler

inte alla vätskepartiklar färdas med samma hastighet i ett rör. Formen på hastighetskurvan (hastighetsprofilen över en viss del av röret) beror på om flödet är laminärt eller turbulent. Om flödet i ett rör är laminärt, kommer hastighetsfördelningen vid ett tvärsnitt att vara parabolisk i form med maximal hastighet i mitten som är ungefär dubbelt så stor som medelhastigheten i röret., I turbulent flöde finns en ganska platt hastighetsfördelning över rörsektionen, vilket resulterar i att hela vätskan strömmar vid ett givet enda värde. Figur 5 hjälper till att illustrera ovanstående idéer. Hastigheten hos vätskan i kontakt med rörväggen är väsentligen noll och ökar längre bort från väggen.

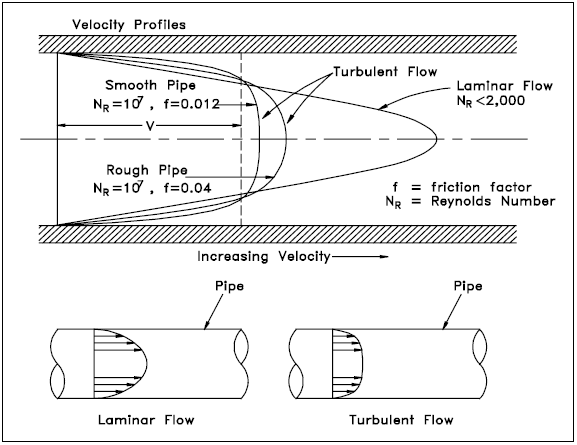
Observera från Figur 5 att hastighetsprofilen beror på rörväggens ytförhållande., En jämnare vägg resulterar i en mer enhetlig hastighetsprofil än en grov rörvägg.

Genomsnittlig (Bulk) hastighet

i många vätskeflödesproblem, istället för att bestämma exakta hastigheter på olika platser i samma flödestvärsnitt, är det tillräckligt att tillåta en enda medelhastighet för att representera hastigheten för all vätska vid den punkten i röret. Detta är ganska enkelt för turbulent flöde eftersom hastighetsprofilen är platt över majoriteten av röret tvärsnitt. Det är rimligt att anta att medelhastigheten är densamma som hastigheten i mitten av röret.,

om flödesregimen är laminär (hastighetsprofilen är parabolisk) finns problemet fortfarande att försöka representera den ”genomsnittliga” hastigheten vid ett visst tvärsnitt eftersom ett medelvärde används i vätskeflödesekvationerna. Tekniskt sett görs detta med hjälp av integrerad kalkyl. Praktiskt taget ska studenten använda ett medelvärde som är hälften av mittlinjevärdet.

viskositet

viskositet är en vätskeegenskap som mäter vätskans motståndskraft mot deformering på grund av skjuvkraft., Viskositet är den inre friktionen av en vätska som gör det motstå flödande förbi en fast yta eller andra skikt av vätskan. Viskositet kan också anses vara ett mått på motståndet hos en vätska till flytande. En tjock olja har en hög viskositet; vatten har en låg viskositet. Måttenhet för absolut viskositet är:

vätskans viskositet är vanligtvis signifikant beroende av vätskans temperatur och relativt oberoende av trycket., För de flesta vätskor, när vätskans temperatur ökar, minskar vätskans viskositet. Ett exempel på detta kan ses i smörjoljan av motorer. När motorn och dess smörjolja är kalla är oljan mycket viskös eller tjock. Efter att motorn startats och smörjoljan ökar i temperatur minskar viskositeten hos oljan avsevärt och oljan verkar mycket tunnare.

idealisk vätska

en idealisk vätska är en som är inkompressibel och har ingen viskositet., Ideala vätskor existerar faktiskt inte, men ibland är det användbart att överväga vad som skulle hända med en idealisk vätska i ett visst vätskeflödesproblem för att förenkla problemet.

Reynolds-nummer

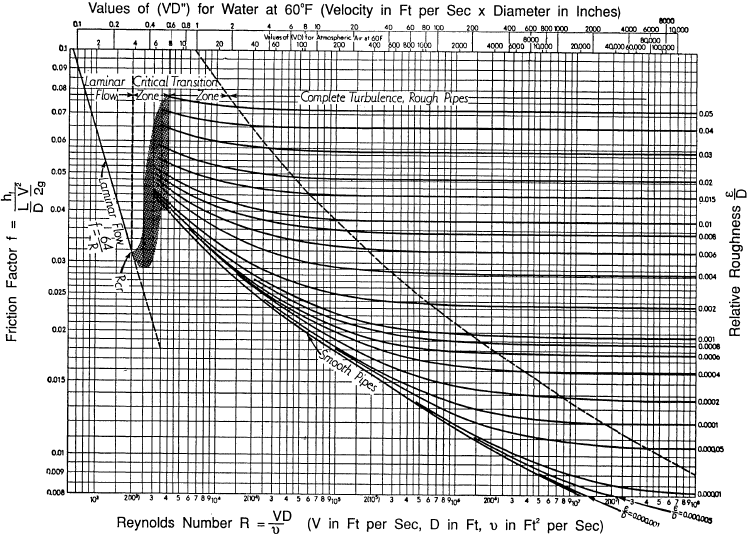
flödesregimen (antingen laminär eller turbulent) bestäms genom utvärdering av flödets Reynolds-nummer (se figur 5). Reynolds-numret, baserat på studier av Osborn Reynolds, är ett dimensionslöst antal bestående av flödets fysiska egenskaper. Ekvation 3-7 används för att beräkna Reynolds-numret (NR) för vätskeflöde.,

var:

för praktiska ändamål, om Reynolds-numret är mindre än 2000, är flödet laminärt. Om det är större än 3500 är flödet turbulent. Flöden med Reynolds-tal mellan 2000 och 3500 kallas ibland övergångsflöden. De flesta vätskesystem i kärnanläggningar fungerar med turbulent flöde. Reynolds-nummer kan bekvämt bestämmas med hjälp av ett Moody-Diagram, vars exempel visas nedan. Ytterligare detaljer om användningen av Moody-diagrammet finns i efterföljande text.,