liksidig triangel form

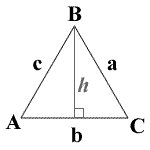
a = vinkel a
a = Sida a
b = vinkel b
b = sida b
C = vinkel C
C = sida C
A = B = C = 60°
a = b = c
k = område
P = omkrets
s = semiperimeter
h = höjd

*längdenheter är för din referens endast eftersom värdet av de resulterande längderna alltid kommer att vara samma oavsett vad enheterna är.,

kalkylator användning

en liksidig triangel är ett specialfall av en triangel där alla 3 sidor har lika längd och alla 3 vinklar är lika med 60 grader. Höjden som visas h är hb eller, höjden av b. för liksidiga trianglar h = ha = hb = hc.

om du har någon 1 känd kan du hitta de andra 4 okända. Så om du känner till längden på en sida = A, eller omkretsen = P, eller semiperimetern = s, eller området = K, eller höjden = h, kan du beräkna de andra värdena. Nedan är de 5 olika val av beräkningar du kan göra med denna liksidiga triangel kalkylator., Låt oss veta om du har några andra förslag!, K och h

med tanke på området hitta sidan, omkrets, semiperimeter och höjd

• k är känd; hitta A, P, S och h
• a = √ = 2 * √
• p = 3a
• s = 3a / 2
• h = (1/2) * √3 * a

med tanke på höjden hitta sidan, omkrets, semiperimeter och område

• H är känd; hitta A, P, S och k
• a = (2 / √3) * h
• p = 3a
• s = 3a / 2
• k = (1/4) * √3 * A2

För mer information om trianglar se: