Når en gratis positive ladningen q er fremskyndet av et elektrisk felt, det er gitt kinetisk energi (Figur \(\PageIndex{1}\))., Prosessen er analogt til et objekt blir akselerert av et gravitasjonsfelt, som om gebyret var å gå ned en elektrisk hill, der elektrisk potensiell energi er omgjort til kinetisk energi, selv om selvfølgelig kilder av kreftene er svært forskjellige. La oss utforske det arbeid som gjøres på en ladning q av det elektriske feltet i denne prosessen, slik at vi kan utvikle en definisjon av elektrisk potensiell energi.

elektrostatisk eller Coulomb force er konservative, noe som betyr at arbeidet som er gjort på q er uavhengige av banen tatt, som vi vil vise senere., Dette er akkurat analogt til gravitasjonskraft. Når en kraft er konservativ, er det mulig å definere en potensiell energi forbundet med makt. Det er vanligvis lettere å arbeide med potensiell energi (fordi det avhenger bare på posisjon) enn å beregne arbeid direkte.

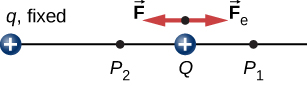
arbeidet \(W_{12}\) utført av anvendt kraft \(\vec{F}\) når partikkelen beveger seg fra \(P_1\) til \(P_2\) kan beregnes ved å

\

\

hvor vi har definert positivt å bli peker bort fra opprinnelsen og r er avstand fra origo. Retningene på både vekt og anvendt kraft i systemet i Figur \(\PageIndex{2}\) er parallelle, og dermed arbeidet som er gjort på systemet er positive.

Vi bruker bokstaven U for å betegne elektrisk potensiell energi, som har enheter i joule (J)., Når en konservativ kraft gjør negative arbeid, systemet får potensiell energi. Når en konservativ kraft har positiv arbeid, systemet mister potensiell energi, \(\Delta U = – W\). I systemet i Figur \(\PageIndex{3}\), den Coulomb kraft virker i motsatt retning i forhold til vekt, og derfor er det arbeid som er negativt. Vi har imidlertid økt potensiell energi i de to-charge system.

I dette eksempelet, er arbeidet W gjort for å akselerere en positiv ladning fra resten er positiv og resultater fra et tap i U, eller en negativ \(\Delta U\)., En verdi for U kan bli funnet på noe som helst tidspunkt ved å ta ett poeng som en referanse og beregning av det arbeidet som trengs for å flytte en ladning til det andre punktet.

Gravitasjonsfelt potensiell energi og elektrisk potensiell energi er ganske analogt. Potensiell energi-kontoer for arbeid utført av en konservativ kraft, og gir økt innsikt om energi og energi transformasjon uten nødvendigheten av å håndtere kraft direkte. Det er mye mer vanlig, for eksempel for å bruke begrepet elektrisk potensiell energi enn å håndtere Coulomb kraft direkte i den virkelige verden programmer.,

\

Merk at Q er en konstant.

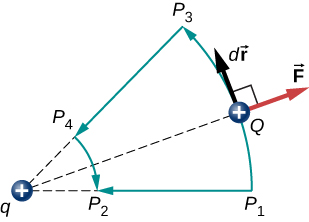
en Annen implikasjon er at vi kan definere en elektrisk potensiell energi. Husker at arbeidet gjort av en konservativ kraft er også uttrykkes som forskjellen i potensiell energi som svarer til den styrken., Derfor er arbeidet \(W_{ref}\) for å få en kostnad fra en referanse punkt til et punkt av interesse kan skrives som

\

og, ved Ligningen \ref{7.1}, forskjellen i potensiell energi (\(U_2 – U_1\)) av testen ladning Q mellom de to punktene er

\

Derfor, vi kan skrive et generelt uttrykk for potensiell energi av to punkt kostnader (i sfæriske koordinater):

\_{r_{ref}}^r = kqQ\venstre.,\]

Vi kan ta det andre begrepet for å være en vilkårlig konstant referanse nivå, som fungerer som null-referanse:

\

Et praktisk valg av referanse som er avhengig av vår vanlige oppfatning er at når de to avgiftene er uendelig langt fra hverandre, er det ingen interaksjon mellom dem. (Husker diskusjon av referanse potensiell energi i Potensiell Energi og Bevaring av Energi., Ta den potensielle energien i denne tilstanden til å være null fjerner begrepet \(U_{ref}\) fra ligning (akkurat som når vi sier bakken er null potensiell energi i et gravitasjonsfelt potensiell energi problem), og den potensielle energien Q når den er skilt fra q-med en avstand r forutsetter form

\

på Grunn av Coulomb er lov, styrker på grunn av flere belastninger på en test lade \(Q\) overlappes, de kan være beregnet individuelt og deretter lagt til. Dette innebærer at arbeidet integraler og derav resulterende potensiell energi viser samme oppførsel., For å demonstrere dette, anser vi et eksempel på å sette sammen et system av fire avgifter.

Merk at elektrisk potensiell energi er positiv hvis de to avgiftene er av samme type, enten positive eller negative, og at negative hvis de to avgiftene er av motsatt typer. Dette er fornuftig hvis du tror på endring i potensiell energi \(\Delta U\) som du tar med de to gebyrer nærmere eller flytter dem lengre fra hverandre., Avhengig av den relative typer kostnader, du kan ha til arbeid på systemet eller system ville gjøre arbeid på deg, det er, er ditt arbeid er enten positive eller negative. Hvis du har å gjøre positive arbeid på systemet (faktisk skyv avgifter nærmere), så energien i systemet skal øke. Hvis du tar to positive ladninger eller to negative ladninger nærmere, du har å gjøre positive arbeid på systemet, som øker sin potensielle energi. Siden potensiell energi er proporsjonal med 1/r, den potensielle energien går opp når r går ned mellom to positive og to negative ladninger.,

På den annen side, hvis du tar med en positiv og en negativ ladning nærmere, du har å gjøre negative arbeid på systemet (kostnader trekker deg), som betyr at du tar energi bort fra systemet. Dette reduserer den potensielle energi. Siden potensiell energi er negativ i tilfelle av en positiv og en negativ ladning par, økningen i 1/r gjør den potensielle energien mer negativ, som er det samme som en reduksjon i potensiell energi.

resultatet fra Eksempel \(\PageIndex{2}\), kan bli utvidet til systemer med noen vilkårlig antall av kostnader., I dette tilfellet er det mest praktisk å skrive formelen som

\

Den faktoren 1/2-kontoer for å legge til hvert par av anklager om to ganger.