Veldig uformelt, de to vilkårene i sum gitt av Black-Scholes formel kan bli tenkt på som «dagens pris av aksjer vektet med sannsynligheten for at du vil benytte deg av muligheten til å kjøpe aksjen «minus» den rabatterte prisen for å utøve alternativ vektet med sannsynligheten for at du vil utøve opsjonen’, eller rett og slett «hva du kommer til å få «minus» hva du kommer til å betale’ (Khan, 2013).,

For en Europeisk salgsopsjon (kontrakter for rett, men ikke plikt, til å selge noen underliggende aktiva til en forhåndsavtalt pris på en forhåndsdefinert dato i framtiden) tilsvarende funksjonell form er:

Eksempel: Beregning av prisen av en Europeisk kjøpsopsjon

for å beregne hva prisen av en Europeisk kjøpsopsjon skal bli, vi vet at vi trenger fem verdier som kreves av ligning 6 ovenfor. De er: 1. Den gjeldende prisen på aksjen (S), 2. Innløsningskurs samtale-alternativet (X), 3. Tiden utløper (T – t), 4. Risikofri rente (r) og 5., Volatiliteten i aksjemarkedet, gitt ved standardavvik av historisk logg avkastning (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

Vi kan beregne noen stock volatilitet er ved å observere sin historiske priser, eller enda enklere, ved å beregne andre alternativet priser for samme lager i forskjellige forfall/utløpsdatoer (T) og øvelse/streik priser (X), hvis vi vet at de er angitt i henhold til en Black-Scholes modellen. Den resulterende verdi, σ, er et nummer mellom 0 og 1, som representerer markedets implisitte volatilitet for aksjen., For Tesla, på tidspunktet for å skrive denne artikkelen, verdien var på ca 0.38 for 4-5 annet alternativ priser rundt samme løpetid/forfall. Innspill til ligning 6 ovenfor, finner vi at samtale-alternativet vi er interessert i, bør være et sted priser rundt $7.

Implisitt volatilitet

Selv om det er interessant for å forstå hvordan valg utstedere kommer til prisen av sine kjøps-og salgsopsjoner, som investorer det er vanskelig å «uenig» med slike priser, per se, og så vanskelig å slå denne kunnskapen i praktisk investering teser.,

Vi kan imidlertid få en mye milage ut av Black-Scholes formelen hvis vi i stedet behandle pris for et alternativ (C eller S) som en kjent mengde/uavhengige variabelen (funnet ved å se på ulike forfall/utløpsdatoer T og annen trening priser X). Dette fordi, hvis vi gjør det, Black-Scholes funksjonelle ligningen blir et verktøy for å hjelpe oss å forstå hvordan markedet estimater volatilitet på et lager, også kjent som implisitt volatilitet av dette alternativet. Dette er informasjon vi kan være uenige i, og handelen mot.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called «continuous timeline instruments”), they are much more difficult to deal with that European options («point in time instruments”)., Først og fremst, siden den optimale utøve politikk vil påvirke verdien av opsjonen, dette må tas i betraktning når du skal løse Black-Scholes partielle ligningen. Det er ingen kjente «lukket form» løsninger for Amerikanske valg i henhold til Black-Scholes-ligningen. Det er skjønt, noen spesielle tilfeller:

• Om Amerikanske valg på underliggende eiendeler som ikke betaler utbytte (eller andre utbetalinger), Amerikansk kjøpsopsjon prisen er den samme som for Eu-valg. Dette fordi den optimale utøve politikk i dette tilfellet er å ikke utøve opsjonen.,
• Om Amerikanske valg på underliggende eiendeler som betaler en kjent utbytte i sin levetid, kan det være optimalt å utøve opsjonen tidlig., I slike tilfeller kan være optimalt utøves like før aksjer går ex utbytte, i henhold til en løsning som er gitt i lukket form av den såkalte Roll-Geske-Whaley metode (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

Først, og sjekk om det er optimalt å utøve opsjonen tidlig, ved å undersøke om følgende ulikhet er oppfylt:

For S = stock price, X = innløsningskurs, D₁ = utbytte, t = dagens dato, t₁ = dato for utbetaling av utbytte, T = utløpsdatoen av opsjonen.

Hvis ulikheten er ikke oppfylt, tidlig utøve den ikke er optimal., Hvis C(・) er den vanlige Black-Scholes formel for Europeiske kjøpsopsjoner på ikke-utbytteutdelende lager (eq x), verdien av den Amerikanske samtale alternativet er da gitt ved en versjon av den samme ligningen hvor aksjekursen (S) er neddiskontert:

Hvis ulikheten er oppfylt, tidlig trening er optimal, og verdien av den Amerikanske call opsjon er gitt ved følgende, forferdelig, rot av en ligning (jeg prøvde å bryte det opp av hver termin å gjøre det mer lesbart):

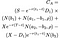
Hvor som før S = pris på lager, T = dato for utløpet av opsjonen, X = innløsningskurs og r = risikofri rente, σ = volatilitet (standardavvik på logg av historisk avkastning for aksjer), og D₁ er utbetaling av utbytte. I tillegg, ρ er gitt ved:

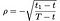
a₁, a₂ by:

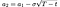
and b₁, b₂ by:

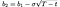
Begrensninger

Det bør gå uten å si at Black-Scholes modellen er nettopp det, en teoretisk modell som forsøker å anslå hvordan et marked fungerer, gitt de forutsetninger som er nevnt ovenfor og den iboende begrensninger av vår egen numeriske beregninger av risikofri rente (r) og fremtidig volatilitet (σ). Det bør her fremheves at ikke alle forutsetninger for (spesielt den opprinnelige modellen) er faktisk empirisk gyldig., For eksempel, betydelige begrensninger oppstår fra:

• undervurdering av ekstreme bevegelser i aksjen, noe som gir halen risiko
• forutsetningen om øyeblikkelig, kostnad mindre handel, som gir likviditetsrisiko
• forutsetningen for en stasjonær prosess, som gir volatilitet risiko
• forutsetningen for kontinuerlig tid og handel, gir gap risiko

Disse skal ivaretas i alle investeringsstrategier, for eksempel ved sikring med out-of-the-money opsjoner, handel på flere børser, sikring med volatilitet sikring og Gamma sikring, henholdsvis.,

Bakgrunn

Som kort nevnte at det var Fischer Svart og Myron Scholes som i 1973 viste at dynamisk å revidere en portefølje i henhold til visse regler fjerner forventet avkastning på underliggende verdipapir (Svart & Scholes, 1973). Deres modell er bygget på tidligere etablerte verker av Bachelier, Samuelson og andre. Robert C. Merton var den første til å publisere et papir å utvide forståelsen av modellen, og som innførte begrepet «Black-Scholes valg prismodell»., Scholes og Merton var tildelt 1997 Nobels minnepris i Økonomisk Vitenskap for deres oppdagelse av metode for skilsmisse opsjoner fra risikoen i de underliggende verdipapirer. Som Fischer-Svart, gikk bort i 1995, ville han ikke være berettiget til å motta prisen, men ble anerkjent som en bidragsyter av Nobels Academy.