Articles

Kommutative, Assosiativ og Distributive Lovene

by admin

Wow! Hva en munnfull av ord! Men ideer er enkelt.

Kommutative Lover

«Kommutative Lover» si at vi kan bytte tall over og fortsatt få samme svar …

… når vi legg til:

a + b = b + a

Eksempel:

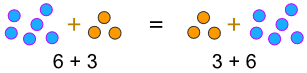
… eller når vi multiplisere:

a × b = b × a

Eksempel:

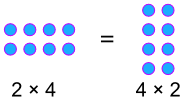
Kommutative Prosenter!,

Fordi a × b = b × a det er også sant at en% av b = b% av en

Eksempel: 8% til 50 = 50% 8, der er 4

Hvorfor «kommutative» … ?

Fordi tallene kan reise frem og tilbake som en pendler.

Assosiativ Lover

«Assosiativ Lover» si at det ikke spiller noen rolle hvor vi gruppere tall (dvs. som beregner vi først) …

…, når vi legg til:

(a + b) + c = a + (b + c)

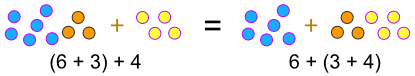
…,r>

Dette: (2 + 4) + 5 = 6 + 5 = 11 Har samme svar som dette: 2 + (4 + 5) = 2 + 9 = 11

Dette: (3 × 4) × 5 = 12 × 5 = 60
Har samme svar som dette: 3 × (4 × 5) = 3 × 20 = 60

Bruker:

noen Ganger er det enklere å legge til eller formere i en annen rekkefølge:

Hva er 19 + 36 + 4?,

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

Eller å omorganisere litt:

Hva er 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

Distributive Loven

«Den Distributive Lov» er den BESTE av alle, men må nøye oppmerksomhet.,

Dette er det som lar oss gjøre:

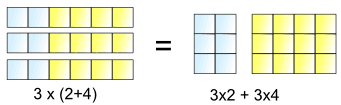
3 masse (2+4) er det samme som 3 massevis av 2 pluss 3 mye 4

Så, 3× kan være «distribuert» over 2+4, i 3×2-og 3×4

Og vi skriver det slik:

a × (b + c) = a × b + a × c

Prøv beregningene deg selv:

  • 3 × (2 + 4) = 3 × 6 = 18
  • 3×2 + 3×4 = 6 + 12 = 18

uansett får det samme svaret.,

I engelsk som vi kan si:

Vi få det samme svaret når vi:

  • multiplisere et tall av en gruppe tall legges sammen, eller
  • gjøre hver multiplisere separat deretter legge dem

Bruker:

noen Ganger er det lettere å bryte opp en vanskelig multiplikasjon:

Eksempel: Hva er 6 × 204 ?

6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224

Eller til å kombinere:

Eksempel: Hva er 16 × 6 + 16 × 4?,

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

Vi kan bruke det i subtraksjon også:

Eksempel: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

Vi kan bruke det for en lang liste med filer, for:

Eksempel: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140

. . . men ikke gå for langt!,

Den Kommutative Loven ikke fungerer for subtraksjon eller divisjon:

Eksempel:

  • 12 / 3 = 4, men
  • 3 / 12 = ¼

Den Assosiative Loven ikke fungerer for subtraksjon eller divisjon: