atunci Când un liber sarcină pozitivă q este accelerată de un câmp electric, este dat energie cinetică (Figura \(\PageIndex{1}\))., Procesul este analog cu un obiect care este accelerat de un câmp gravitațional, ca și cum sarcina ar coborî pe un deal electric unde energia sa potențială electrică este transformată în energie cinetică, deși, desigur, sursele forțelor sunt foarte diferite. Să explorăm activitatea desfășurată pe o sarcină q de către câmpul electric în acest proces, astfel încât să putem dezvolta o definiție a energiei potențiale electrice.forța electrostatică sau Coulomb este conservatoare, ceea ce înseamnă că munca efectuată pe q este independentă de calea luată, așa cum vom demonstra mai târziu., Acest lucru este exact analog cu forța gravitațională. Atunci când o forță este conservatoare, este posibil să se definească o energie potențială asociată cu forța. De obicei, este mai ușor să lucrați cu energia potențială (deoarece depinde doar de poziție) decât să calculați direct lucrarea.

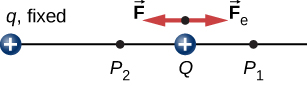
lucrarea \(W_{12}\) făcut de forța aplicată \(\vec{F}\), atunci când o particulă se deplasează de la \(P_1\) a \(P_2\) poate fi calculată prin

\

\

în cazul în care am definit pozitiv să fie îndreptată departe de originea și r este distanța de la origine. Direcțiile atât ale deplasării, cât și ale forței aplicate în sistem în figura \(\PageIndex{2}\) sunt paralele și astfel munca efectuată asupra sistemului este pozitivă.

folosim litera U pentru a desemna energia potențială electrică, care are unități de jouli (J)., Atunci când o forță conservatoare nu funcționează negativ, sistemul câștigă energie potențială. Când o forță conservatoare funcționează pozitiv, sistemul pierde energia potențială, \(\Delta U = – W\). În sistemul din Figura \(\PageIndex{3}\), forța Coulomb acționează în direcția opusă deplasării; prin urmare, lucrarea este negativă. Cu toate acestea, am crescut energia potențială în sistemul cu două încărcări.

în acest exemplu, munca w făcută pentru a accelera o sarcină pozitivă din repaus este pozitivă și rezultă dintr-o pierdere în U sau un negativ \(\Delta U\)., O valoare pentru U poate fi găsită în orice punct, luând un punct ca referință și calculând munca necesară pentru a muta o încărcare în celălalt punct.energia potențială gravitațională și energia potențială electrică sunt destul de analoage. Energia potențială reprezintă munca depusă de o forță conservatoare și oferă o perspectivă suplimentară asupra transformării energiei și a energiei fără necesitatea de a face față direct forței. Este mult mai frecvent, de exemplu, să se utilizeze conceptul de energie potențială electrică decât să se facă față forței Coulomb direct în aplicațiile din lumea reală.,

\

rețineți că Q este o constantă.

o altă implicație este că putem defini o energie potențială electrică. Amintiți-vă că munca făcută de o forță conservatoare este, de asemenea, exprimată ca diferența de energie potențială corespunzătoare acestei forțe., Prin urmare, activitatea \(W_{ref}\) pentru a aduce o încărcătură dintr-un punct de referință de la un punct de interes poate fi scris ca

\

și, de Ecuație \ref{7.1}, diferența de energie potențială (\(U_2 – U_1\)) de la testul de sarcina Q între două puncte este

\

prin Urmare, se poate scrie o expresie generală pentru energie potențială de două sarcini punctiforme (în coordonatele sferice):

\_{r_{ref}}^r = kqQ\stânga.,putem considera că al doilea termen este un nivel arbitrar de referință constant, care servește ca referință zero:

\

o alegere convenabilă de referință care se bazează pe bunul nostru simț este că atunci când cele două sarcini sunt infinit de îndepărtate, nu există nicio interacțiune între ele. (Reamintim discuția despre energia potențială de referință în energia potențială și conservarea energiei.,) Având potențialul de energie din acest stat să fie zero elimină termenul \(U_{ref}\) din ecuația (ca atunci când spunem sol este zero energie potențială în energie potențială gravitațională problemă), și energia potențială a Q atunci când este separat de q printr-o distanță r își asumă forma

\

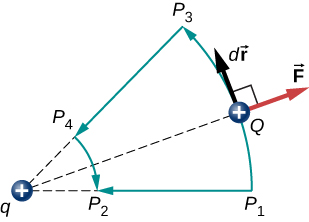
Datorita legea lui Coulomb, forțele din cauza mai multe acuzații la un test de încărcare \(Q\) suprapune; ele pot fi calculate individual și apoi a adăugat. Aceasta implică faptul că integralele de lucru și, prin urmare, energiile potențiale rezultate prezintă același comportament., Pentru a demonstra acest lucru, considerăm un exemplu de asamblare a unui sistem de patru taxe.

Rețineți că potențialul electric de energie este pozitiv dacă cele două acuzații sunt de același tip, fie negativ sau pozitiv, și negativ, dacă cele două acuzații sunt de tipuri opuse. Acest lucru are sens dacă vă gândiți la schimbarea energiei potențiale \(\Delta U\) Pe măsură ce aduceți cele două încărcături mai aproape sau le mutați mai departe., În funcție de tipurile relative de taxe, poate fi necesar să lucrați la sistem sau sistemul ar lucra la dvs., adică munca dvs. este fie pozitivă, fie negativă. Dacă trebuie să faceți o muncă pozitivă asupra sistemului (împingeți de fapt taxele mai aproape), atunci energia sistemului ar trebui să crească. Dacă aduceți mai aproape două sarcini pozitive sau două sarcini negative, trebuie să faceți o muncă pozitivă asupra sistemului, ceea ce le ridică energia potențială. Deoarece energia potențială este proporțională cu 1 / r, Energia potențială crește atunci când r coboară între două sarcini pozitive sau două negative.,pe de altă parte, dacă aduceți o încărcare pozitivă și una negativă mai aproape, trebuie să faceți o muncă negativă asupra sistemului (taxele vă trag), ceea ce înseamnă că luați energie departe de sistem. Acest lucru reduce energia potențială. Deoarece energia potențială este negativă în cazul unei perechi de sarcină pozitivă și negativă, creșterea în 1/r face ca energia potențială să fie mai negativă, ceea ce este același cu o reducere a energiei potențiale.

rezultatul de la Example \(\PageIndex{2}\) poate fi extins la sisteme cu orice număr arbitrar de taxe., În acest caz, este cel mai convenabil să scrieți formula ca

\

factorul de 1/2 conturi pentru adăugarea fiecărei perechi de taxe de două ori.