Foarte informal, cei doi termeni din suma dată de formula Black-Scholes poate fi gândit ca ‘prețul actual de valori ponderate cu probabilitatea pe care o va exercita opțiunea de a cumpăra acțiuni „minus” a redus prețul de exercitare a opțiunii ponderată cu probabilitatea pe care o va exercita opțiunea’, sau pur și simplu ce-ai de gând să mă „minus” ce aveți de gând să plătească’ (Khan, 2013).,

Pentru un European opțiune put (contracte pentru dreptul, dar nu obligația, de a vinde unele underlaying activ la un preț prestabilit pe o pre-stabilit data în viitor) echivalentul formă funcțională este:

Exemplu: Calcularea prețului de o opțiune call Europeană

pentru a calcula prețul de opțiune call Europeană ar trebui să fie, știm că avem nevoie de cinci valori cerute de ecuația 6 de mai sus. Acestea sunt: 1. Prețul curent al acțiunilor, 2. Prețul de exercitare al opțiunii de apel (X), 3. Timpul până la expirare (T – t), 4. Rata dobânzii fără risc (r) și 5., Volatilitatea stocului, dată de abaterea standard a randamentelor jurnalelor istorice (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

putem estima orice stoc volatilitatea observându prețurile istorice, sau, mai simplu, prin calcularea altă opțiune prețurile pentru același stoc la diferite scadența/termenul de expirare (T) și de exercițiu/prețuri de exercitare (X), dacă știm că au fost configurate pentru un Black-Scholes. Valoarea rezultată, σ, este un număr între 0 și 1, reprezentând volatilitatea implicită a pieței pentru stoc., Pentru Tesla, la momentul scrierii acestui articol, valoarea medie a fost de aproximativ 0.38 pentru 4-5 prețuri diferite de opțiuni în jurul aceleiași date de expirare / scadență. Introduceți în ecuația 6 de mai sus, constatăm că opțiunea de apel care ne interesează ar trebui să fie prețuri undeva în jurul valorii de $7.deși este interesant să înțelegem modul în care emitenții de opțiuni ajung la prețul apelului lor și pun opțiuni, ca investitori este greu să „nu sunt de acord” cu astfel de prețuri, în sine, și atât de dificil de a transforma aceste cunoștințe în teze de investiții acționabile.,

cu toate acestea, putem obține o mulțime de milage din formula Black-Scholes dacă tratăm în schimb prețul unei opțiuni (C sau P) ca o cantitate cunoscută/variabilă independentă (găsită analizând diferite date de scadență/expirare T și diferite prețuri de exercițiu X). Acest lucru deoarece, dacă o facem, ecuația funcțională Black-Scholes devine un instrument care ne ajută să înțelegem modul în care piața estimează volatilitatea unui stoc, cunoscută și sub numele de volatilitatea implicită a opțiunii. Aceasta este o informație pe care nu o putem contrazice și împotriva comerțului.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called „continuous timeline instruments”), they are much more difficult to deal with that European options („point in time instruments”)., În primul rând, deoarece politica optimă de exerciții va afecta valoarea opțiunii, aceasta trebuie luată în considerare la rezolvarea ecuației diferențiale parțiale Black-Scholes. Nu există soluții cunoscute de „formă închisă” pentru opțiunile americane conform ecuației Black-Scholes. Există, totuși, câteva cazuri speciale:

• pentru opțiunile de apel americane pe active subiacente care nu plătesc dividende (sau alte plăți), prețul opțiunii de apel americane este același ca și pentru opțiunile de apel Europene. Acest lucru deoarece politica optimă de exerciții în acest caz este de a nu exercita opțiunea.,
• pentru opțiunile de apel americane asupra activelor subiacente care plătesc un dividend cunoscut în timpul vieții sale, poate fi optimă exercitarea opțiunii din timp., În astfel de cazuri, opțiunea poate fi optim exercitat doar înainte ca bursa ex-dividend, conform soluției date în formă închisă de către așa-numita Geske-Whaley metoda (Rola, 1977; Geske, 1979; 1981; Whaley, 1981):

în Primul rând, verificați dacă este optim să-și exercite opțiunea de timpuriu, de a investiga dacă următoarele inegalitatea este îndeplinită:

Pentru S = prețul de vînzare, X = prețul de exercitare, în care d₁ = dividend plătit, t = data curentă, t₁ = data plății dividendelor, T = data de expirare a opțiunii.dacă inegalitatea nu este îndeplinită, exercitarea timpurie nu este optimă., Dacă C(・) este regulat Black-Scholes formula Europene opțiunile de apel non-dividende-plăți de valori (eq x), valoarea American opțiune call este dat de o versiune de aceeași ecuație în cazul în care prețul de vînzare (S) este redus:

Dacă inegalitatea este îndeplinită, la începutul exercițiu este optimă și valoarea American opțiune call este dat de următoarele, groaznic, mizerie de o ecuație (am încercat să-i despartă de către fiecare termen pentru a face mai ușor de citit):

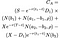
în cazul în Care ca și mai înainte S = prețul de stoc, T = data de expirare a opțiunii, X = preț de exercitare și r = rata dobânzii fără risc, σ = volatilitatea (abaterea standard de jurnal de istoric se întoarce din stoc), și în care d₁ este plata dividendelor. În plus, ρ este dat de:

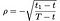
a₁, a₂ by:

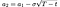
and b₁, b₂ by:

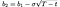
Limitări

Acesta ar trebui să meargă fără a spune că modelul Black-Scholes este exact asta, un model teoretic care încearcă să estimeze cât o piață se comportă, având în vedere ipotezele menționate mai sus și limitările inerente ale noastre proprii numerice estimări ale ratelor dobânzilor fără risc (r) și volatilitatea viitoare (σ). Aici trebuie subliniat faptul că nu toate ipotezele (în special modelul original) sunt de fapt valabile empiric., De exemplu, limitări semnificative apar de la:

• subestimarea de miscari extreme în stoc, obținându-coada de risc
• ipoteza instant, costul-mai puțin de tranzacționare, rezultând riscul de lichiditate
• ipoteza unui proces staționar, rezultând riscul de volatilitate
• ipoteza în timp continuu și de comercializare, rezultând diferența de risc

Acestea ar trebui să fie reprezentat în orice și toate strategiile de investiții, de exemplu prin acoperire cu out-of-the-bani opțiuni de tranzacționare pe mai multe schimburi, acoperire cu volatilitate acoperire și Gama de acoperire, respectiv.,după cum am menționat Pe scurt, Fischer Black și Myron Scholes au arătat în 1973 că revizuirea dinamică a unui portofoliu în conformitate cu anumite reguli elimină randamentul așteptat al securității subiacente (Negru & Scholes, 1973). Modelul lor a fost construit pe lucrări stabilite anterior de Bachelier, Samuelson și alții. Robert C. Merton a fost primul care a publicat o lucrare care se extinde asupra înțelegerii modelului și care a inventat termenul „model de prețuri pentru opțiunile Black-Scholes”., Scholes și Merton au primit Premiul Nobel Memorial în științe Economice din 1997 pentru descoperirea metodei de divorț a opțiunilor de acțiuni de riscul titlurilor de valoare subiacente. Deoarece Fischer Black a murit în 1995, el nu ar fi eligibil pentru a primi premiul, dar a fost recunoscut ca contribuitor de către Academia Nobel.