Legile comutative, asociative și Distributive
Wow! Ce gura plina de cuvinte! Dar ideile sunt simple.
legile comutative
„legile comutative” spun că putem schimba numerele și obținem același răspuns …
… când adăugăm:
a + b = b + a
exemplu:
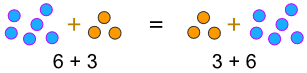
… sau când înmulțim:
a × b = b × a
exemplu:
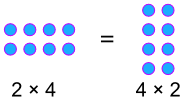
procente comutative!,
Pentru a × b = b × a este, de asemenea, adevărat că o% a b = b% a o
Exemplu: 8% din 50 = 50% din 8, care este de 4

de Ce „comutativ” … ?deoarece numerele pot călători înainte și înapoi ca un navetist.
legile asociative
„legile asociative” spun că nu contează cum grupăm numerele (adică pe care le calculăm mai întâi) …
…, când adăugăm:
(a + b) + c = a + (b + c)
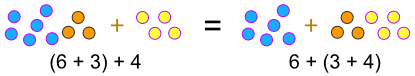
…,r>
| Acest lucru: | (3 × 4) × 5 = 12 × 5 = 60 |
| Are același răspuns ca acesta: | 3 × (4 × 5) = 3 × 20 = 60 |
Utilizare:
Uneori este mai ușor să adăugați sau să se multiplice într-o ordine diferită:
Ce este 19 + 36 + 4?,
19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59
sau pentru a rearanja un pic:
ce este 2 × 16 × 5?
2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160
Legea distributivă
„Legea distributivă” este cea mai bună dintre toate, dar are nevoie de o atenție atentă.,
Aceasta este ceea ce ne permite să facem:
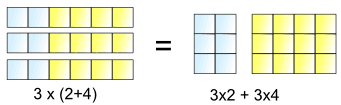
3 o mulțime de (2+4) este la fel ca 3 loturi de 2 plus 3 loturi de 4
Deci, 3× pot fi „distribuite” de peste 2+4, în 3×2 și 3×4
Și vom scrie astfel:
a × (b + c) = a × b + a × c
Încercați calculele te:
- 3 × (2 + 4) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
oricum primeste acelasi raspuns., în engleză putem spune:
obținem același răspuns atunci când:
- înmulțim un număr cu un grup de numere adăugate împreună sau
- facem fiecare înmulțire separat, apoi le adăugăm
utilizări:
uneori este mai ușor să spargem o înmulțire dificilă:
exemplu: ce este 6 × 204?
6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224
sau pentru a combina:
exemplu: Ce este 16 × 6 + 16 × 4?,
16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160
putem folosi în scădere prea.
Exemplu: 26×3 – 24×3
= 2 × 3
= 6
Ne-am putea folosi pentru o lungă lista de completări, de asemenea:
Exemplu: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140
. . . dar nu merge prea departe!,
Legea comutativă nu funcționează pentru scădere sau divizare:
exemplu:
- 12 / 3 = 4, dar
- 3 / 12 = ¼
Legea asociativă nu funcționează pentru scădere sau divizare:















